http://www.scribd.com/doc/90799213/Tugas-Teori-Bahasa-Dan-Automata
Tampilkan postingan dengan label Materi Kuliah. Tampilkan semua postingan
Tampilkan postingan dengan label Materi Kuliah. Tampilkan semua postingan
Senin, 18 Juni 2012
Pemahaman dan Sejarah Otomata
Otomata
Teori Bahasa dan Otomata
Bahasa adalah struktur yang dikendalikan sekumpulan aturan tertentu, semacam mesin untuk memproduksi makna. Akan tetapi seperti setiap mesin hanya terdapat kemungkinan terbatas bagi setiap orang dalam menggunakannya.
Dalam bahasa disediakan pembendaharaan kata atau tanda (vocabulary), serta perangkat aturan bahasa (grammar, sintaks) yang harus dipatuhi jika hendak menghasilkan sebuah ekspresi yang bermakna.
Proses Kemampuan Pemahaman Bahasa
Hipotesis Noam Chomsky menggugat postulat John Locke (tokoh empirisme) yang menyatakan segala pengetahuan yang dimiliki manusia berasal dari rangsangan-rangsangan luar (pengalaman) yang ditangkap oleh indera-indera manusia, sehingga meniadakan pengetahuan apriori (pengetahuan yang langsung tertanam di manusia)
Noam Chomsky menyandarkan pada pemahaman bahasa sebagai sesuatu yang bersifat khas dan bawaan (tertanam) pada manusia sejak lahir.
Secara khusus Chomsky dipengaruhi Descartes tentang bahasa dan pikiran yang terikat begitu erat sehingga pengetahuan tentang bahasa bisa membuka pengetahuan tentang pikiran manusia.
Secara mendasar bahasa adalah bagian psikologi manusia yang dipahami sebagai teori tentang kemampuan pikiran manusia berupa ungkapan dari subjek psikologi.
Chomsky dan para ahli bahasa telah mengamati anak kecil mampu menjadi lancar berbahasa lebih cepat dan mudah dibanding "algoritma belajar berbahasa".
Sehingga para ahli bahasa membuat hipotesis otak berisi/memuat suatu "mesin bahasa umum". Kemudian selama masa awal pertumbuhan anak, terjadi pertemuan dengan bahasa sehari-hari yang mengubah mesin bahasa umum menjadi mesin bahasa partikular (tertentu) ke bahasa spesifik.
Teori Bahasa
Teori Bahasa adalah konsep-konsep pada "string alpabet V" dalam penyambungan karakter-karakter alpabet untuk membentuk suatu makna (bahasa).
- Alpabet
Adalah himpunan simbol (karakter) tak kosong yang berhingga. Alpabet digunakan untuk membentuk kata-kata (string-string) di bahasa. Bahasa dimulai dengan alpabet. Pada beberapa buku, alpabet dilambangkan dengan Σ
Istilah huruf, karakter dan simbol adalah sinonim menunjukkan elemen alpabet. Jika simbol berbaris bersebelahan, maka diperoleh "string simbol". Istilah kalimat, kata dan string adalah sinonim
Contoh :
{a,b} -> Himpunan yang terdiri dari simbol "a" dan "b".
- Penyambungan (Concatenation - o)
Penyambungan dilakukan pada 2 karakter atau lebih membentuk 1 barisan karakter (string simbol).
Contoh :
'a' o 'b' = 'ab'
'ab' o 'baab' = 'abbaab'
- String pada alpabet V
Karakter atau barisan karakter pada alpabet V dibentuk dari penyambungan karakter pada alpabet V.
String pada alpabet V adalah deretan (sekeun) simbol dari V dimana perulangan simbol diijinkan.
Contoh :
V = {a,b,c,d}
String pada alpabet V antara lain -> 'a','abcd','bbba'
Pemangkatan
Penyambungan dapat dianggap sebagai perkalian karena biasanya penulisannya adalah bila x dan y string, maka x o y adalah xy. sehingga pemangkatan dapat digunakan
VoV = VV = V2 ----> Panjang string = 2
VoVoV = V2oV=V3 -> Panjang string = 3
VoVoVoV = N4 ----> Panjang string = 4
VoVoVo...oV=Vn ---> Panjang string = n
Vk = VoVoVo...oV
adalah himpunan string dengan panjang k, masing-masing simbol adalah alpabet V
V* = {ε} U V+ (Kleene closure)
adalah string pada V, termasuk string kosong dimana ε string kosong (string tanpa simbol)
ε mempunyai sifat identitas, yaitu:
ε o x = x
x o ε = x
V+ = V1 U V2 U V3 U ... (Positive closure)
adalah himpunan string pada V, tidak ada string kosong didalamnya.
V0 = {ε}
adalah himpunan yang isinya hanya string kosong, dimana String kosong ε tidak sama dengan himpunan kosong �
Maka 'bbba' dapat ditulis 'b3a'
Panjang String
Panjang string dilambangkan |w| dimana panjang string adalah jumlah simbol di dalam string bukan pada alpabet dan pengulangan kemunculan simbol dihitung.
Contoh:
|ε| = 0
|a| = 1
|aa| = 2
|aaa| = 3
|aaab| = 4
Otomata
Otomata adalah mesin abstrak yang menggunakan model matematika, tetapi matematika yang digunakan benar-benar berbeda dibanding matematika klasik dan kalkulus. Model yang digunakan adalah model mesin state (state machine model) atau model trnasisi state (state transition model).
Terdapat 3 model komputasi pada teori otomata.
- Finite automata
- Pushdown automata
- Turing Mavhine
Memori Otomata
Otomata dibedakan berdasarkan jenis memori sementara yang dimilikinya, yaitu:
- Finite automata (FA)
Tidak memiliki memori sementara. Finite automata adalah kelas mesin dengan kemampuan-kemampuan paling terbatas.
- Pushdown automata (PDA)
Memiliki memori sementara dengan mekanisme LIFO (Last In, First Out). Mesin ini lebih ampuh karena bantuan keberadaan stack yang dipandang sebagai unit memori
- Turing Machine (TM)
Memiliki memori dengan mekanisme pengaksesan acak (Random akses memori). Turing Machine merupakan model matematika untuk komputer saat ini.
Sejarah Otomata dan Teori Bahasa
Otomata bermula sebelum komputer ada pada teori di bidang sistem logika matematika atau formal, ilmuwan David Hilbert telah mencoba menciptakan algoritma umum untuk pembuktian (seluruh) persoalan matematika secara otomatis yaitu mampu menentukan salah benarnya sembarang prosisi matematika.
Tahun 1931, Kurt G�del mempublikasikan teori ketidaklengkapan dimana membuktikan prosedur/algoritma yang dikehendaki David Hilbert tersebut tidak akan pernah ada.
G�del membangun rumus di kalkulus predikat yang diterapkan pada bilangan bulat yang memiliki pernyataan-pernyataan definisi yang tidak dapat dibuktikan maupun dibantah di dalam sistem logika yang mungkin dibangun manusia.
Formalisasi argumen teorema ketidaklengkapan G�del ini berikut penjelasan dan formalisasi selanjutnya dari prosedur efektif secara intuisi merupakan salah satu pencapaian intelektual terbesar abad 20, yaitu abad dimana formalisasi berkembang semarak.
Pengembangan teori otomata, komputasi dan teori bahasa berikutnya difasilitasi perkembangan bidang psyco-linguistic. Bidang psyco-linguistic berupaya menjawab pertanyan-pertanyan berikut:
- Apakah bahasa secara umum?
- Bagaimana manusia mengembangkan bahasa?
- Bagaimana manusia memahami bahasa?
- Bagaimana manusia mengajarkan bahasa ke anak-anaknya?
- Apa gagasan-gagasan yang dapat dinyatakan dan bagaimana caranya?
- Bagaimana manusia membangun kalimat-kalimat dari gagasan-gagasan yang berada di pikirannya?
Sekitar tahun 1950-an, Noam Chomsky menciptakan model matematika sebagai sarana untuk mendeskripsikan bahasa serta menjawab pertanyaan-pertanyaan di atas. Saat ini dimulai pendalaman bidang bahasa komputer.
Perbedaan antara bahasa komputer dan bahasa manusia adalah sampai sekarang belum diketahuinya bagaimana cara manusia mengartikan bahasa, sementara dengan pasti dapat mengartikan bahasa pada komputer.
Noam Chomsky mengemukakan perangkat format disebut grammar untuk memodelkan properti-properti bahasa.
Grammar berisi sejumlah aturan serta menspesifikasikan bahasa tertentu.
Bahasa berisi semua string yang dapat dihasilkan menggunakan aturan-aturan grammar.
Meski pembahasan Chomsky terutama ditujukan untuk bahasa alami, grammar mempunyai nilai/manfaat sangat besar di ilmu informatika/komputer karena pencapaian ini digunakan untuk mendeskripsikan dan mendefinisikan sintaks bahasa pemrograman dan bahasa-bahasa formal lainnya.
Grammar diterapkan pada perancangan kompilator dan bidang-bidang di ilmu komputer.
McCulloch dan Pitts mengemukakan Mesin Abstrak sederhana yaitu finite automata untuk memodelkan neuron nets.
Finite automata juga digunakan untuk merancang switching circuit. Studi mengenai teori otomata terkait bidang-bidang lain di ilmu komputer.
Kemudian ekivalensi antara finite automata dan ekspresi reguler (reguler expression) dikemukakan Stephen Kleene. Sejak saat itu teori bahasa dikaitkan secara erat dengan teori bahasa formal. ubungan teori otomata dan teori pengkodean (coding theory) juga banyak diteliti.
Turing machine seperti komputer modern saat ini dapat mengolah (simbol-simbol di tape) dan mengahasilkan keluaran (simbol-simbol yang berada di tapenya setelah berakhirnya sebarisan pergerakkan) merupakan karya teoritis dari Alan Turing.
Karena banyak yang berperan pada pengembangannya, bidang teori ini diberi aneka ragam nama yaitu:
- teori otomata (theory of automata)
- teori bahasa formal (theory of formal language)
- teori mesin turing (theory of Turing machine).
Bahasa adalah struktur yang dikendalikan sekumpulan aturan tertentu, semacam mesin untuk memproduksi makna. Akan tetapi seperti setiap mesin hanya terdapat kemungkinan terbatas bagi setiap orang dalam menggunakannya.
Dalam bahasa disediakan pembendaharaan kata atau tanda (vocabulary), serta perangkat aturan bahasa (grammar, sintaks) yang harus dipatuhi jika hendak menghasilkan sebuah ekspresi yang bermakna.
Proses Kemampuan Pemahaman Bahasa
Hipotesis Noam Chomsky menggugat postulat John Locke (tokoh empirisme) yang menyatakan segala pengetahuan yang dimiliki manusia berasal dari rangsangan-rangsangan luar (pengalaman) yang ditangkap oleh indera-indera manusia, sehingga meniadakan pengetahuan apriori (pengetahuan yang langsung tertanam di manusia)
Noam Chomsky menyandarkan pada pemahaman bahasa sebagai sesuatu yang bersifat khas dan bawaan (tertanam) pada manusia sejak lahir.
Secara khusus Chomsky dipengaruhi Descartes tentang bahasa dan pikiran yang terikat begitu erat sehingga pengetahuan tentang bahasa bisa membuka pengetahuan tentang pikiran manusia.
Secara mendasar bahasa adalah bagian psikologi manusia yang dipahami sebagai teori tentang kemampuan pikiran manusia berupa ungkapan dari subjek psikologi.
Chomsky dan para ahli bahasa telah mengamati anak kecil mampu menjadi lancar berbahasa lebih cepat dan mudah dibanding "algoritma belajar berbahasa".
Sehingga para ahli bahasa membuat hipotesis otak berisi/memuat suatu "mesin bahasa umum". Kemudian selama masa awal pertumbuhan anak, terjadi pertemuan dengan bahasa sehari-hari yang mengubah mesin bahasa umum menjadi mesin bahasa partikular (tertentu) ke bahasa spesifik.
Teori Bahasa
Teori Bahasa adalah konsep-konsep pada "string alpabet V" dalam penyambungan karakter-karakter alpabet untuk membentuk suatu makna (bahasa).
- Alpabet
Adalah himpunan simbol (karakter) tak kosong yang berhingga. Alpabet digunakan untuk membentuk kata-kata (string-string) di bahasa. Bahasa dimulai dengan alpabet. Pada beberapa buku, alpabet dilambangkan dengan Σ
Istilah huruf, karakter dan simbol adalah sinonim menunjukkan elemen alpabet. Jika simbol berbaris bersebelahan, maka diperoleh "string simbol". Istilah kalimat, kata dan string adalah sinonim
Contoh :
{a,b} -> Himpunan yang terdiri dari simbol "a" dan "b".
- Penyambungan (Concatenation - o)
Penyambungan dilakukan pada 2 karakter atau lebih membentuk 1 barisan karakter (string simbol).
Contoh :
'a' o 'b' = 'ab'
'ab' o 'baab' = 'abbaab'
- String pada alpabet V
Karakter atau barisan karakter pada alpabet V dibentuk dari penyambungan karakter pada alpabet V.
String pada alpabet V adalah deretan (sekeun) simbol dari V dimana perulangan simbol diijinkan.
Contoh :
V = {a,b,c,d}
String pada alpabet V antara lain -> 'a','abcd','bbba'
Pemangkatan
Penyambungan dapat dianggap sebagai perkalian karena biasanya penulisannya adalah bila x dan y string, maka x o y adalah xy. sehingga pemangkatan dapat digunakan
VoV = VV = V2 ----> Panjang string = 2
VoVoV = V2oV=V3 -> Panjang string = 3
VoVoVoV = N4 ----> Panjang string = 4
VoVoVo...oV=Vn ---> Panjang string = n
Vk = VoVoVo...oV
adalah himpunan string dengan panjang k, masing-masing simbol adalah alpabet V
V* = {ε} U V+ (Kleene closure)
adalah string pada V, termasuk string kosong dimana ε string kosong (string tanpa simbol)
ε mempunyai sifat identitas, yaitu:
ε o x = x
x o ε = x
V+ = V1 U V2 U V3 U ... (Positive closure)
adalah himpunan string pada V, tidak ada string kosong didalamnya.
V0 = {ε}
adalah himpunan yang isinya hanya string kosong, dimana String kosong ε tidak sama dengan himpunan kosong �
Maka 'bbba' dapat ditulis 'b3a'
Panjang String
Panjang string dilambangkan |w| dimana panjang string adalah jumlah simbol di dalam string bukan pada alpabet dan pengulangan kemunculan simbol dihitung.
Contoh:
|ε| = 0
|a| = 1
|aa| = 2
|aaa| = 3
|aaab| = 4
Otomata
Otomata adalah mesin abstrak yang menggunakan model matematika, tetapi matematika yang digunakan benar-benar berbeda dibanding matematika klasik dan kalkulus. Model yang digunakan adalah model mesin state (state machine model) atau model trnasisi state (state transition model).
Terdapat 3 model komputasi pada teori otomata.
- Finite automata
- Pushdown automata
- Turing Mavhine
Memori Otomata
Otomata dibedakan berdasarkan jenis memori sementara yang dimilikinya, yaitu:
- Finite automata (FA)
Tidak memiliki memori sementara. Finite automata adalah kelas mesin dengan kemampuan-kemampuan paling terbatas.
- Pushdown automata (PDA)
Memiliki memori sementara dengan mekanisme LIFO (Last In, First Out). Mesin ini lebih ampuh karena bantuan keberadaan stack yang dipandang sebagai unit memori
- Turing Machine (TM)
Memiliki memori dengan mekanisme pengaksesan acak (Random akses memori). Turing Machine merupakan model matematika untuk komputer saat ini.
Sejarah Otomata dan Teori Bahasa
Otomata bermula sebelum komputer ada pada teori di bidang sistem logika matematika atau formal, ilmuwan David Hilbert telah mencoba menciptakan algoritma umum untuk pembuktian (seluruh) persoalan matematika secara otomatis yaitu mampu menentukan salah benarnya sembarang prosisi matematika.
Tahun 1931, Kurt G�del mempublikasikan teori ketidaklengkapan dimana membuktikan prosedur/algoritma yang dikehendaki David Hilbert tersebut tidak akan pernah ada.
G�del membangun rumus di kalkulus predikat yang diterapkan pada bilangan bulat yang memiliki pernyataan-pernyataan definisi yang tidak dapat dibuktikan maupun dibantah di dalam sistem logika yang mungkin dibangun manusia.
Formalisasi argumen teorema ketidaklengkapan G�del ini berikut penjelasan dan formalisasi selanjutnya dari prosedur efektif secara intuisi merupakan salah satu pencapaian intelektual terbesar abad 20, yaitu abad dimana formalisasi berkembang semarak.
Pengembangan teori otomata, komputasi dan teori bahasa berikutnya difasilitasi perkembangan bidang psyco-linguistic. Bidang psyco-linguistic berupaya menjawab pertanyan-pertanyan berikut:
- Apakah bahasa secara umum?
- Bagaimana manusia mengembangkan bahasa?
- Bagaimana manusia memahami bahasa?
- Bagaimana manusia mengajarkan bahasa ke anak-anaknya?
- Apa gagasan-gagasan yang dapat dinyatakan dan bagaimana caranya?
- Bagaimana manusia membangun kalimat-kalimat dari gagasan-gagasan yang berada di pikirannya?
Sekitar tahun 1950-an, Noam Chomsky menciptakan model matematika sebagai sarana untuk mendeskripsikan bahasa serta menjawab pertanyaan-pertanyaan di atas. Saat ini dimulai pendalaman bidang bahasa komputer.
Perbedaan antara bahasa komputer dan bahasa manusia adalah sampai sekarang belum diketahuinya bagaimana cara manusia mengartikan bahasa, sementara dengan pasti dapat mengartikan bahasa pada komputer.
Noam Chomsky mengemukakan perangkat format disebut grammar untuk memodelkan properti-properti bahasa.
Grammar berisi sejumlah aturan serta menspesifikasikan bahasa tertentu.
Bahasa berisi semua string yang dapat dihasilkan menggunakan aturan-aturan grammar.
Meski pembahasan Chomsky terutama ditujukan untuk bahasa alami, grammar mempunyai nilai/manfaat sangat besar di ilmu informatika/komputer karena pencapaian ini digunakan untuk mendeskripsikan dan mendefinisikan sintaks bahasa pemrograman dan bahasa-bahasa formal lainnya.
Grammar diterapkan pada perancangan kompilator dan bidang-bidang di ilmu komputer.
McCulloch dan Pitts mengemukakan Mesin Abstrak sederhana yaitu finite automata untuk memodelkan neuron nets.
Finite automata juga digunakan untuk merancang switching circuit. Studi mengenai teori otomata terkait bidang-bidang lain di ilmu komputer.
Kemudian ekivalensi antara finite automata dan ekspresi reguler (reguler expression) dikemukakan Stephen Kleene. Sejak saat itu teori bahasa dikaitkan secara erat dengan teori bahasa formal. ubungan teori otomata dan teori pengkodean (coding theory) juga banyak diteliti.
Turing machine seperti komputer modern saat ini dapat mengolah (simbol-simbol di tape) dan mengahasilkan keluaran (simbol-simbol yang berada di tapenya setelah berakhirnya sebarisan pergerakkan) merupakan karya teoritis dari Alan Turing.
Karena banyak yang berperan pada pengembangannya, bidang teori ini diberi aneka ragam nama yaitu:
- teori otomata (theory of automata)
- teori bahasa formal (theory of formal language)
- teori mesin turing (theory of Turing machine).
Mesin Turing
Mesin Turing
Dari Wikipedia bahasa Indonesia, ensiklopedia bebas
Belum Diperiksa
Mesin Turing adalah model komputasi teoritis yang ditemukan oleh Alan Turing, berfungsi sebagai model ideal untuk melakukan perhitungan matematis. Walaupun model ideal ini diperkenalkan sebelum komputer nyata dibangun, model ini tetap diterima kalangan ilmu komputer sebagai model komputer yang sesuai untuk menentukan apakah suatu fungsi dapat selesaikan oleh komputer atau tidak (menentukan computable function). Mesin Turing terkenal dengan ungkapan " Apapun yang bisa dilakukan oleh Mesin Turing pasti bisa dilakukan oleh komputer."
Sebuah mesin turing terdiri atas barisan sel tersusun berupa pita yang dapat bergerak maju mundur, komponen aktif baca/tulis pita yang memiliki status perhitungan serta dapat mengubah/menulisi sel aktif yang ada di pita tadi, dan suatu kumpulan instruksi bagaimana komponen baca/tulis ini harus melakukan modifikasi terhadap sel aktif pada pita, serta bagaimana menggerakkan pita tersebut. Pada setiap langkah dalam komputasi, mesin ini akan dapat mengubah isi dari sel yang aktif, mengubah status dari komponen baca/tulis, dan mengubah posisi pita kekiri atau kekanan.
[sunting]Langton's ant, a simple two-dimensional analogue of the Turing machine.Lihat pula
- Probabilistic Turing machine
- Church-Turing thesis, which says Turing machines can perform any computation that can be performed.
- Busy Beaver
- Computability logic
- Turing completeness
- Turing tarpit, any computing system or language which, like the Turing machine, is not only Turing-complete but also useless for practical computing.
- Neal Stephenson's Cryptonomicon
[sunting]Referensi
- Rolf Herken: The Universal Turing Machine - A Half-Century Survey, Springer Verlag, ISBN 3-211-82637-8
- Paul Strathern: Turing and the Computer - The big idea, Anchor Books/Doubleday, ISBN 0-385-49243-X
- Turing, A., On Computable Numbers, With an Application to the Entscheidungsproblem, Proceedings of the London Mathematical Society, Series 2, Volume 42, 1936; reprinted in M. David (ed.), The Undecidable, Hewlett, NY: Raven Press, 1965;
- Boolos, G. and Jeffrey, R., Computability and Logic, 2nd ed., Cambridge: Cambridge University Press, 1980.
- Rogozhin, Yurii, "A Universal Turing Machine with 22 States and 2 Symbols", Romanian Journal Of Information Science and Technology, 1(3), 259-265, 1998. (surveys known results about small universal Turing machines)
- Wolfram, Stephen, A New Kind of Science, Wolfram Media, ISBN 1-57955-008-8
[sunting]Pranala luar
Konsep Dasar (otomata)
Konsep Dasar
• Anggota alfabet dinamakan simbol terminal.
• Kalimat adalah deretan hingga simbol-simbol terminal.
• Bahasa adalah himpunan kalimat-kalimat. Anggota bahasa bisa tak hingga kalimat.
• Simbol-simbol berikut adalah simbol terminal :
- huruf kecil, misalnya : a, b, c
- simbol operator, misalnya : +, , dan *
- simbol tanda baca, misalnya : (, ), dan ;
- simbol tanda baca, misalnya : (, ), dan ;
- string yang tercetak tebal, misalnya : if, then, dan else.
• Simbol-simbol berikut adalah simbol non terminal /Variabel :
- huruf besar, misalnya : A, B, C
- huruf S sebagai simbol awal
- string yang tercetak miring, misalnya : expr
• Huruf yunani melambangkan string yang tersusun atas simbol-simbol terminal atau simbol-simbol non terminal atau campuran keduanya, misalnya : α,β, dan ε
• Sebuah produksi dilambangkan sebagai α --> β, artinya : dalam sebuah derivasi dapat dilakukan penggantian simbol α dengan simbol β.
• Derivasi adalah proses pembentukan sebuah kalimat atau sentensial. Sebuah derivasi dilambangkan sebagai : α ==> β.
• Sentensial adalah string yang tersusun atas simbol-simbol terminal atau simbol-simbol non terminal atau campuran keduanya.
• Kalimat adalah string yang tersusun atas simbol-simbol terminal. Kalimat adalah merupakan sentensial, sebaliknya belum tentu.. Grammar :
Grammar G didefinisikan sebagai pasangan 4 tuple : Vt , Vn , S, dan P, dan dituliskan sebagai G(Vt , Vn , S, P), dimana :
Vt : himpunan simbol-simbol terminal (alfabet) = kamus Vn : himpunan simbol-simbol non terminal S C V : simbol awal (atau simbol start) P : himpunan produksi
Contoh :
1. G1 : VT = {I, want, need, You}, V = {S,A,B,C}, P = {S --> ABC, A--> I, B--> want | need, C--> You}
S --> ABC
--> IwantYou
L(G1)={IwantYou,IneedYou}
2. . G2 : VT = {a}, V = {S}, P = {S aS | a}
S --> aS
--> aaS
--> aaa L(G2) ={an --> n ≥ 1}
L(G2)={a, aa, aaa, aaaa,…}
[sunting]Otomata Berhingga
bisa bantu ga???
[sunting]Definisi Formal
Otomata adalah sebuah 5-tupel  :
:
 :
: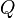 adalah himpunan berhingga dari state,
adalah himpunan berhingga dari state, adalah himpunan simbol-simbol,
adalah himpunan simbol-simbol, adalah fungsi transisi
adalah fungsi transisi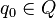 adalah simbol awal
adalah simbol awal adalah state akhir
adalah state akhir
[sunting]Jenis-jenis Otomata Berhingga
[sunting]Otomata Berhingga Deterministik
Otomata berhingga deterministik (DFA - Deterministic Finite Automata) adalah sebuah otomata yang fungsi transisinya adalah:
[sunting]Otomata Berhingga Non-Deterministik
Otomata berhingga non-deterministik (NFA - Nondeterministic Finite Automata) berbeda dengan DFA dalam hal fungsi transisinya:
Fungsi transisi dalam NFA memetakan pasangan 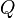 dan
dan  kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
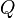 dan
dan  kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.[sunting]Otomata Pushdown
Otomata Pushdown adalah salah satu varian otomata dengan 7-tupel 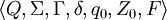 , di mana:
, di mana:
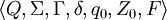 , di mana:
, di mana: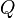 adalah himpunan berhingga dari state,
adalah himpunan berhingga dari state, adalah himpunan simbol-simbol,
adalah himpunan simbol-simbol,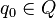 adalah simbol awal
adalah simbol awal adalah state akhir
adalah state akhir
Ditambah dengan dua unsur, untuk menangani stack:
 adalah himpunan berhingga simbol-simbol stack,
adalah himpunan berhingga simbol-simbol stack, adalah simbol awal stack,
adalah simbol awal stack,
Dengan fungsi transisinya adalah
 adalah fungsi transisi
adalah fungsi transisi
[sunting]Otomata Terbatas Linear
[sunting]Mesin Turing
[sunting]Hubungan dengan Tata Bahasa
Setiap otomata berhingga dapat digunakan untuk mengenali bahasa tertentu.
[sunting]Referensi
- John E. Hopcroft, Jeffrey D. Ullman - Introduction to Automata Theory, Languages, and Computation
| Artikel bertopik matematika ini adalah sebuah rintisan. Anda dapat membantu Wikipedia dengan mengembangkannya. |
Langganan:
Postingan (Atom)