Konsep Dasar
• Anggota alfabet dinamakan simbol terminal.
• Kalimat adalah deretan hingga simbol-simbol terminal.
• Bahasa adalah himpunan kalimat-kalimat. Anggota bahasa bisa tak hingga kalimat.
• Simbol-simbol berikut adalah simbol terminal :
- huruf kecil, misalnya : a, b, c
- simbol operator, misalnya : +, , dan *
- simbol tanda baca, misalnya : (, ), dan ;
- simbol tanda baca, misalnya : (, ), dan ;
- string yang tercetak tebal, misalnya : if, then, dan else.
• Simbol-simbol berikut adalah simbol non terminal /Variabel :
- huruf besar, misalnya : A, B, C
- huruf S sebagai simbol awal
- string yang tercetak miring, misalnya : expr
• Huruf yunani melambangkan string yang tersusun atas simbol-simbol terminal atau simbol-simbol non terminal atau campuran keduanya, misalnya : α,β, dan ε
• Sebuah produksi dilambangkan sebagai α --> β, artinya : dalam sebuah derivasi dapat dilakukan penggantian simbol α dengan simbol β.
• Derivasi adalah proses pembentukan sebuah kalimat atau sentensial. Sebuah derivasi dilambangkan sebagai : α ==> β.
• Sentensial adalah string yang tersusun atas simbol-simbol terminal atau simbol-simbol non terminal atau campuran keduanya.
• Kalimat adalah string yang tersusun atas simbol-simbol terminal. Kalimat adalah merupakan sentensial, sebaliknya belum tentu.. Grammar :
Grammar G didefinisikan sebagai pasangan 4 tuple : Vt , Vn , S, dan P, dan dituliskan sebagai G(Vt , Vn , S, P), dimana :
Vt : himpunan simbol-simbol terminal (alfabet) = kamus Vn : himpunan simbol-simbol non terminal S C V : simbol awal (atau simbol start) P : himpunan produksi
Contoh :
1. G1 : VT = {I, want, need, You}, V = {S,A,B,C}, P = {S --> ABC, A--> I, B--> want | need, C--> You}
S --> ABC
--> IwantYou
L(G1)={IwantYou,IneedYou}
2. . G2 : VT = {a}, V = {S}, P = {S aS | a}
S --> aS
--> aaS
--> aaa L(G2) ={an --> n ≥ 1}
L(G2)={a, aa, aaa, aaaa,…}
[sunting]Otomata Berhingga
bisa bantu ga???
[sunting]Definisi Formal
Otomata adalah sebuah 5-tupel  :
:
 :
: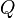 adalah himpunan berhingga dari state,
adalah himpunan berhingga dari state, adalah himpunan simbol-simbol,
adalah himpunan simbol-simbol, adalah fungsi transisi
adalah fungsi transisi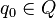 adalah simbol awal
adalah simbol awal adalah state akhir
adalah state akhir
[sunting]Jenis-jenis Otomata Berhingga
[sunting]Otomata Berhingga Deterministik
Otomata berhingga deterministik (DFA - Deterministic Finite Automata) adalah sebuah otomata yang fungsi transisinya adalah:
[sunting]Otomata Berhingga Non-Deterministik
Otomata berhingga non-deterministik (NFA - Nondeterministic Finite Automata) berbeda dengan DFA dalam hal fungsi transisinya:
Fungsi transisi dalam NFA memetakan pasangan 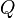 dan
dan  kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
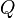 dan
dan  kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.
kepada himpunan kuasa dari Q. Fungsi transisi yang didefinisikan seperti ini memungkinkan suatu simbol masukan untuk mengakibatkan transisi dari sebuah state ke beberapa kemungkinan state yang lain.[sunting]Otomata Pushdown
Otomata Pushdown adalah salah satu varian otomata dengan 7-tupel 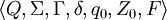 , di mana:
, di mana:
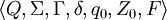 , di mana:
, di mana: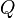 adalah himpunan berhingga dari state,
adalah himpunan berhingga dari state, adalah himpunan simbol-simbol,
adalah himpunan simbol-simbol,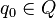 adalah simbol awal
adalah simbol awal adalah state akhir
adalah state akhir
Ditambah dengan dua unsur, untuk menangani stack:
 adalah himpunan berhingga simbol-simbol stack,
adalah himpunan berhingga simbol-simbol stack, adalah simbol awal stack,
adalah simbol awal stack,
Dengan fungsi transisinya adalah
 adalah fungsi transisi
adalah fungsi transisi
[sunting]Otomata Terbatas Linear
[sunting]Mesin Turing
[sunting]Hubungan dengan Tata Bahasa
Setiap otomata berhingga dapat digunakan untuk mengenali bahasa tertentu.
[sunting]Referensi
- John E. Hopcroft, Jeffrey D. Ullman - Introduction to Automata Theory, Languages, and Computation
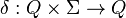

Tidak ada komentar:
Posting Komentar